Manchmal sind weniger Straßen mehr

Mittlerweile beginnt das Leben – trotz Corona – wieder gewohnte Wege einzuschlagen. So stand ich neulich abends in der Bremer Überseestadt im Stau und stellte mir aus purer Langeweile einige Fragen: Warum ist das hier immer so – das kann doch nicht nur an der Brücke liegen? Wieso staut sich der Verkehr von einer Ampel zur nächsten? Gibt es einfach zu viele Kreuzungen? Und ginge das vielleicht schneller, wenn da weniger wären?

Tatsächlich gibt es mit dem „Braess Paradoxon“ ein Gedankenspiel aus der Spieltheorie, das – vereinfacht gesagt – zeigt, dass mehr Straßen manchmal zu längeren Reisezeiten führen können. Und das liegt daran, dass alle Verkehrsteilnehmenden immer die Option wählen, die für sie selbst am vorteilhaftesten ist – und nicht die, die für alle am besten wäre. Möchten Sie eine der Grundlagen der Spieltheorie am Beispiel „Feierabendverkehr“ kennenlernen?

Die Ausgangssituation

Stellen Sie sich vor, es gäbe zwei Städte, Stadt A und Stadt D.

Genau mittig zwischen den beiden Städten gäbe es ein sehr schwer zu überwindendes Hindernis, zum Beispiel einen Berg. Auf beiden Seiten des Hindernisses lägen direkt daneben die beiden Orte B und C. Von der Stadt A kann man nun über zwei mögliche Routen zur Stadt D gelangen.

• Von A kann man über die nördliche Route mit der Autobahn 1 zu Ort C kommen, diese Autobahn umfährt das Hindernis sehr großflächig und ist mehrspurig ausgebaut. Danach kommt man von Ort "C" über eine sich windende schmale Landstraße 1 zu Stadt D. Auf der Landstraße gibt es häufig Stau, weil sie teilweise nicht für das Verkehrsaufkommen ausgebaut ist.
• Auf der anderen Seite gelangt man über die südliche Route über die Landstraße 2 zu Ort B. Genauso wie auf der Landstraße 1 kommt es aber auch hier häufig zu Staus. Danach kann man von B über die Autobahn 2 nach D gelangen. Genauso wie Autobahn 1 führt diese großflächig am Hindernis vorbei und ist gut mehrspurig ausgebaut.

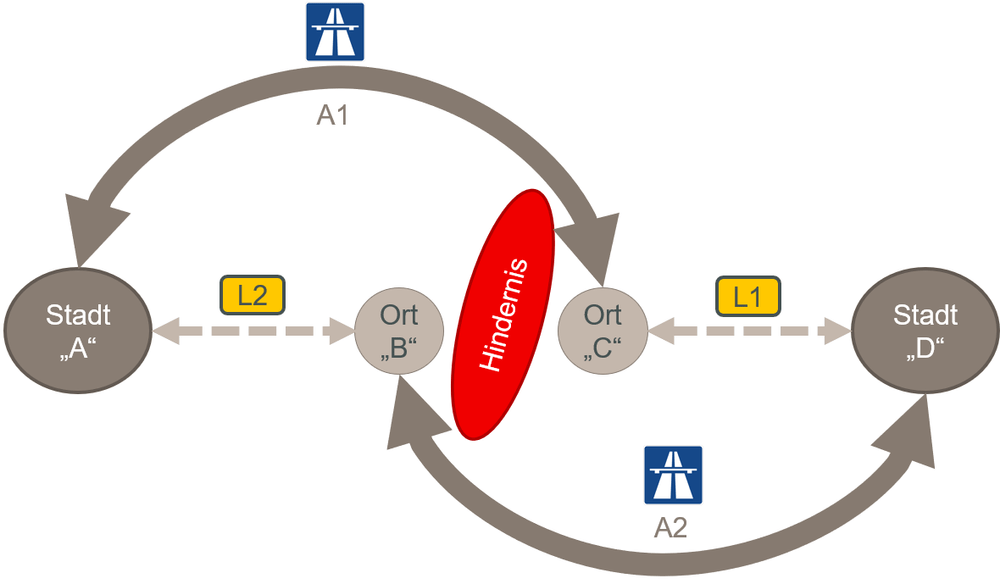
Bei den beiden Autobahnen dauert die durchschnittliche Reisezeit immer 45 Minuten und ist nicht von der Anzahl der darauf fahrenden Autos abhängig, da das Hindernis großräumig umfahren wird.

Bei den beiden Landstraßen ist die Reisezeit abhängig von der Anzahl der darauf fahrenden Autos: Die Straßen sind schmal und schlängeln sich mit vielen Kurven durch die Landschaft. Im Durchschnitt errechnet sich die benötigte Zeit aus der Anzahl der Autos geteilt durch 100.

Egal ob nördliche oder südliche Route: Man braucht für die gesamte Reise (𝒙/𝟏𝟎𝟎+𝟒𝟓)𝒎𝒊𝒏… also zum Beispiel 50 Minuten bei 500 Autofahrern oder 65 Minuten bei 2000 Fahrern.

Zur „Rush Hour“ auf der nördlichen und südlichen Route

Stellen Sie sich vor, dass zur abendlichen Rushhour 4000 Autos von Stadt A zurück nach Stadt D wollen. Ein Teil der Fahrer wird die nördliche und der andere die südliche Route wählen. Da die Situation auf den Landstraßen die Reisedauer bestimmt, werden entweder die Fahrtzeiten identisch sein, weil jeweils ähnlich viele Fahrzeuge unterwegs sind, oder eine Route ist schneller, da dort weniger fahren. Das spricht sich dann aber mit Sicherheit herum, und am nächsten Tag wechseln einige Fahrer auf die vermeintlich schnellere Route.

Dieses System wird über eine gewisse Zeit hin- und herschwingen, bis die Anzahl der Fahrzeuge auf beiden Strecken mehr oder weniger identisch ist. Dieses Gleichgewicht ist in diesem System die bestmögliche Variante für alle Teilnehmer. In der Spieltheorie nennt man es das "Nash-Gleichgewicht".

In unserem Beispiel fahren also jeweils 2000 Fahrzeuge über die nördliche und ebenso viele über die südliche Route. Alle brauchen im Durchschnitt 65 Minuten (𝟐𝟎𝟎𝟎/𝟏𝟎𝟎+𝟒𝟓)𝐦𝐢𝐧 = (𝟐𝟎+𝟒𝟓)𝐦𝐢𝐧=𝟔𝟓 𝒎𝒊𝒏).

Eine vermeintliche Verbesserung

Um die Zeit zu verkürzen, wird eine direkte Straße durch das Hindernis hindurch gebaut.

Mal angenommen, es kostet keine Zeit, über diese neue Straße X zu fahren, dann haben alle Fahrzeuge, die von A nach D wollen, auf einen Schlag zwei weitere Routen zur Verfügung:

• Sie können nun die komplette Strecke über die beiden Autobahnen A1 und A2 zurücklegen (A1-X-A2) und brauchen dafür 90 Minuten. (𝟒𝟓𝐦𝐢𝐧+𝟒𝟓𝐦𝐢𝐧=𝟗𝟎 𝒎𝒊𝒏)
• Oder sie können die ganze Strecke über die beiden Landstraßen L1 und L2 fahren (L2-X-L1) und benötigen 𝒙𝟏/𝟏𝟎𝟎𝐦𝐢𝐧+𝒙𝟐/𝟏𝟎𝟎𝒎𝒊𝒏 (x1 = Anzahl der Fahrer über die L1; x2 = Anzahl der Fahrer über die L2).

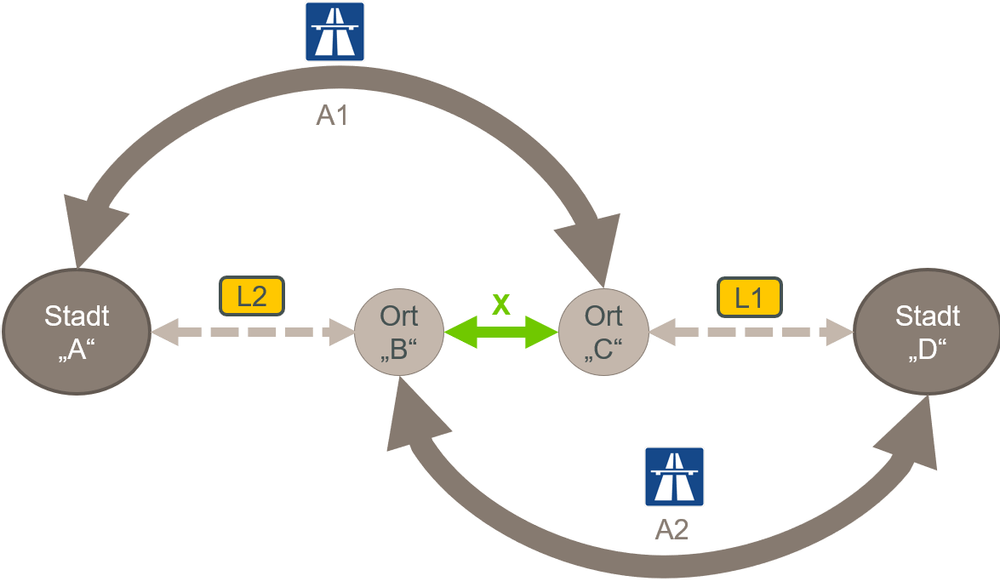
Wie werden sich die Pendler verhalten, die vorher die nördliche oder südliche Route gefahren sind und dafür 65 Minuten gebraucht haben?

• Über die Autobahnen A1-X-A2 wird sicherlich niemand fahren, da die Route in jedem Fall 25 Minuten länger dauert als die bisherige nördliche oder südliche Route.
• Alle Fahrer könnten wie gehabt in 65 Minuten über die „alte“ nördliche oder südliche Route fahren. Aber das wird eher nicht passieren, denn…
• Sehr viel wahrscheinlicher wird wenigstens ein Fahrer etwa der nördlichen Route begreifen, dass er nun statt über die A1 auch über die L2 und dann wie gehabt die L1 fahren kann und damit nur ca. 40 Minuten braucht (𝟐𝟎𝟎𝟎/𝟏𝟎𝟎𝐦𝐢𝐧+𝟐𝟎𝟎𝟏/𝟏𝟎𝟎𝐦𝐢𝐧=𝒄𝒂.𝟒𝟎 𝒎𝒊𝒏).

Ein Zeitgewinn von satten 25 Minuten!

• Andere Fahrer auf der nördlichen Route werden das auch schnell begreifen und sehr bald folgen 499 weitere dem Beispiel. Dann dauert die Fahrt schon 45 Minuten. (𝟐𝟎𝟎𝟎/𝟏𝟎𝟎𝐦𝐢𝐧+𝟐𝟓𝟎𝟎/𝟏𝟎𝟎𝐦𝐢𝐧=𝟐𝟎 𝒎𝒊𝒏+𝟐𝟓𝒎𝒊𝒏=𝟒𝟓 𝒎𝒊𝒏).
• Je mehr Autofahrer von der nördlichen Route auf die L2 wechseln, desto länger wird aber nun hier die Fahrtzeit: Für die „klassische“ südliche Route werden das 70 Minuten, da auf der L2 nun mehr Verkehr ist (𝟐𝟓𝟎𝟎/𝟏𝟎𝟎𝐦𝐢𝐧+𝟒𝟓 𝐦𝐢𝐧=𝟐𝟓 𝒎𝒊𝒏+𝟒𝟓𝒎𝒊𝒏=𝟕𝟎 𝒎𝒊𝒏).
• Durch diesen Zeitverlust werden sicher einige Fahrer von dieser Route auf die L2-X-L1-Route wechseln. Das führt nun wiederum für andere zu einer Verschlechterung der Fahrzeit auf der nördlichen Route, was dort wieder Fahrer veranlasst, auf die L2-X-L1-Route zu wechseln....

Ein Teufelskreis!

Das Nash-Gleichgewicht in diesem neuen System tritt erst dann auf, wenn alle Fahrer über die Route L2-X-L1 fahren. In unserem Beispiel dauert das 80 Minuten! (𝟒𝟎𝟎𝟎/𝟏𝟎𝟎𝐦𝐢𝐧+𝟒𝟎𝟎𝟎/𝟏𝟎𝟎 𝐦𝐢𝐧=𝟒𝟎 𝒎𝒊𝒏+𝟒𝟎𝒎𝒊𝒏=𝟖𝟎 𝒎𝒊𝒏)

Das Paradoxe

Und hier liegt das „Braess-Paradoxon“: Bevor die neue Straße zwischen B und C gebaut wurde, lag die durchschnittliche Reisezeit bei 65 Minuten. Nach dem Bau der neuen Straße bei 80 Minuten. In diesem Beispiel wären alle Verkehrsteilnehmer ohne die neue Straße X schneller am Ziel.

Menschen wählen eher die Option, die für sie selbst am günstigsten ist – in diesem Fall eine Ersparnis von wenigen Minuten – als sich zum Besten Aller zu verhalten.

Dieses Gedankenspiel erklärt aber nicht nur die Theorie, sondern auch, warum in der Praxis manchmal nach der Schließung von großen Verkehrsadern das befürchtete Chaos ausblieb:

• In Seoul war lange Zeit der „Cheonggyecheon“ Highway eine wichtige Verkehrsader durch das Zentrum der Stadt. Im Jahr 2005 wurde er komplett entfernt und in ein grünes Naherholungsgebiet umgewandelt. Das von manchen befürchtete Verkehrschaos blieb aus, tatsächlich verbesserte sich die Verkehrssituation insgesamt.
• 1990 hat die zeitweilige Schließung der 42. Straße in New York zu einer generellen Verbesserung des Verkehrsflusses geführt.
• In Stuttgart kam es 1969 nach Ausbau des Straßennetzes rund um den Schlossplatz zu Verkehrsproblemen, die erst wieder durch die Umwandlung eines Teils der Königsstraße in eine Fußgängerzone abgemildert wurden.

Welche Straße muss weg?

Mit genügend Computerleistung könnten wir vorausberechnen, wie Autofahrer ihr Verhalten ändern würden, wenn wir aus einem komplexen Straßennetz eine einzelne Straße entfernen. Die Kunst besteht aber darin herausfinden, welche Straße – in meinem Fall in der Überseestadt – überhaupt zu entfernen wäre, damit ich und viele andere nicht weiter im Stau stehen müssen. Das allerdings würde uns schnell an physische Grenzen bringen: Wir haben zur Berechnung hiervon keinen wirklich effizienten Algorithmus und müssen alles simulieren. Wenn wir alle Kombinationen möglicher Straßensperrungen in einer Stadt einfach durchprobieren wollten, dann wären das bei einem Straßennetz von „nur“ 80 Straßen theoretisch aber schon mehr zu prüfende Kombinationen (2 hoch 80) als es Sterne im Universum gibt (10 hoch 22) – Nicht machbar innerhalb eines Menschenlebens mit heutigen Rechnerkapazitäten.

Bei der Geschwindigkeit, mit der diese aber im Moment wachsen, ist das vielleicht aber nur eine Frage der Zeit. Vielleicht aber auch nicht.

Bevor ich also das nächste Mal zum Feierabend im Stau stehe, überlege ich mir also am besten mit gesundem Menschenverstand eine Alternative. Vielleicht fahre ich doch lieber mit dem Rad…